初一有理数是什么意思/初一的有理数

学了初一上册数学第一课有理数写篇200字上的收获

在学习初一上册数学第一课有理数后，我获得了以下收获：有理数的定义理解：有理数是可以表示为两个整数之比的数，即形如a/b的数。这让我对有理数有了更直观的认识，明白了它既包括整数，也包括分数。有理数与无理数的区别：无理数是不能表示为两个整数之比的数，如π、e等。

初一语文的第一课是《阳光灿烂的日子》，这节课旨在引导学生走进文学的世界，感受文字的魅力。课堂上，学生们不仅学习了这篇课文的内容，还通过讨论和分析，理解了作者的情感表达方式。数学课则是《有理数的加法和减法》，这节课程让学生们初步掌握了有理数的运算规则，为后续学习打下了坚实的基础。

数轴上的点与有理数的关系：所有的有理数都可以用数轴上的点来表示，正有理数可用原点右边的点表示，负有理数可用原点左边的点表示，0用原点表示。所有的有理数都可以用数轴上的点表示出来，但数轴上的点不都表示有理数。

首先第一课我们认真的学习了教师的师德修养，和教师的职业道德等方面的内容，这些内容是我们作为一位教师，特别是想成为一位好都师所必备的基本素养，通过学习，也使我知道了很多做一位好教师的基本条件。我也一定会认真学习，以身作责的。

初一数学的第一课内容涵盖了有理数的学习，包括负数、数轴、不同类型的数之间的大小比较（如负数与负数、负数与正数、正数与正数）以及绝对值的概念。有理数是整数、分数以及它们的表示形式，通过这些概念的学习，学生能够更好地理解和处理现实生活中的数值问题。

初一有理数知识点归纳有哪些?

〖A〗、相反数：一个数与它的相反数相加等于0。例如，5的相反数是-5，-3的相反数是3。绝对值：一个数到0的距离称为该数的绝对值。绝对值用“| |”表示，如|5|=5，|-3|=3。倒数：一个数与它的倒数的乘积等于1（注意0没有倒数）。例如，5的倒数是1/5，-2的倒数是-1/2。

〖B〗、正有理数可以用原点右边的点表示，负有理数可以用原点左边的点表示，零用原点表示。 利用数轴比较有理数的大小： 在数轴上表示的两个数，右边的数总比左边的数大。正数都大于0；负数都小于0；正数大于一切负数。

〖C〗、初一上册数学人教版知识要点归纳总结如下：有理数 概念与定义： 正数、负数、有理数的定义。 数轴、原点、绝对值的概念。 运算法则： 有理数的加法法则，包括同号相加、异号相加、与0相加。 有理数的减法法则，即减去一个数等于加上这个数的相反数。

〖D〗、数轴：用直线上的点表示数，这条直线叫做数轴。数轴的三要素：原点、正方向、单位长度。相反数：只有符号不同的两个数叫做互为相反数。0的相反数还是0。绝对值：正数的绝对值是它本身，负数的绝对值是它的相反数；0的绝对值是0，两个负数，绝对值大的反而小。

〖E〗、整数：包括正整数、0和负整数。分数：即非整数的有理数，可以表示为两个整数的比。有理数的性质：封闭性：有理数与有理数进行加、减、乘、除运算后，结果仍然是有理数。顺序性：有理数之间可以比较大小，具有序关系。稠密性：在任意两个有理数之间都存在无数个有理数。

什么叫做有理数和无理数???

〖A〗、有理数的定义：有理数是可以被清晰定义为整数或者可以表示为两个整数比的数。这些数的数值可以无限循环或者以有限的方式重复，例如分数2/有限小数22等。无理数的定义：无理数是实数中的另一类数，它们的数值是无限不循环的，无法精确地用分数表示。常见的无理数有π、e等。

〖B〗、有理数是指可以表示为两个整数比值的数，而无理数则是无法表示为两个整数比值的数，即无限不循环小数。有理数的具体特点： 表示方式：有理数可以表示为两个整数的比值，如整数、分数等。 实例：整数5可以看作是5除以1的结果，是一个有理数；分数3/4也是有理数。

〖C〗、有理数： 有理数是指能精确地表示为两个整数之比的数。 例如，9172727272……、7/22都是有理数。 整数和通常所说的分数都是有理数。有理数还可以划分为正有理数、0和负有理数。有理式： 有理式是代数式的一种，包括分式和整式。

〖D〗、有理数是可以表示为两个整数之比的数，包括整数和分数；无理数则是实数范围内不能表示为两个整数之比的数，即无限不循环小数。区分有理数和无理数的方法主要有以下几点：小数形式：有理数：可以写成有限小数或无限循环小数。例如，4=0，4/5=0.8，1/3=0.33333……。

〖E〗、数字不是冰冷的，是活生生的，充满烟火气的，是劳动人民经过实践生活发明的。整数和分数合在一起，我们就统称为有理数。无限循环小数都可以表示成分数，所以它也属于有理数。来看一个不太严谨的计算：0.6767……化成分数等于几？无理数 毕达哥拉斯，古希腊数学家、哲学家。

〖F〗、无理数是指实数范围内不能表示成两个整数之比的数。无理数最早由毕达哥拉斯学派弟子希伯索斯发现，他提出“万物皆为数”的观点：数的元素就是万物的元素，世界是由数组成的，世界上的一切没有不可以用数来表示的，数本身就是世界的秩序。

【初中数学】人教版初一七年级上册数学有理数知识点归纳

有理数的概念 有理数的定义：有理数是可以表示为两个整数之比的数，即形如a/b（b≠0）的数。有理数包括整数、正有理数、负有理数。整数：包括正整数、0和负整数。正有理数：大于0的有理数。负有理数：小于0的有理数。有理数的性质 相反数：一个数与它的相反数相加等于0。例如，5的相反数是-5，-3的相反数是3。

人教版初一七年级上册数学有理数知识点归纳如下：有理数的定义：有理数是可以表示为两个整数之比的数，形如a/b。有理数的分类：整数：包括正整数、0和负整数。分数：即非整数的有理数，可以表示为两个整数的比。

第一章 有理数 正数和负数：理解了正数、负数的概念，知道0既不是正数也不是负数。能用正负数表示实际问题中具有相反意义的量。有理数：理解了有理数的概念，有理数包括整数和分数。掌握了有理数的分类，即正有理数、0、负有理数。

有理数都可以用数轴上的点来表示。相反数：只有符号不同的两个数互为相反数，零的相反数是零。绝对值：一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。有理数的加减法：同号两数相加，取相同的符号，并把绝对值相加。

人教版七年级上册数学知识点总结：有理数：有理数的定义与分类：有理数是可以表示为两个整数之比的数，包括正有理数、负有理数和0。有理数的运算：掌握有理数的加、减、乘、除运算，特别是涉及符号的规则。绝对值：理解绝对值的定义，能求一个数的绝对值。

知识点概览 有理数 概念与性质：理解有理数的定义，掌握有理数的分类（正数、负数、零）、相反数、绝对值等概念。有理数的运算：熟练掌握有理数的加、减、乘、除运算，以及乘方运算，理解运算的法则和性质。代数式 代数式的概念：理解代数式的定义，掌握代数式的书写规则和简化方法。

初一数学上有理数无理数定义

〖A〗、进入到八年级，我们进一步学习了无理数的概念。无理数是指那些无限不循环的小数。无理数可以分为两类：正无理数和负无理数。如圆周率π，根号2（√2）、根号3（√3）以及根号10（√10）都是常见的无理数例子。有理数与无理数共同构成了实数的范畴。实数包括所有的有理数和无理数。

〖B〗、无理数 无理数，也称为无限不循环小数，不能写作两整数之比。见的无理数有：圆周长与其直径的比值，欧拉数e，黄金比例φ等等。实数 实数，是有理数和无理数的总称。数学上，实数定义为与数轴上的实数，点相对应的数。实数可以直观地看作有限小数与无限小数，实数和数轴上的点一一对应。

〖C〗、无理数是指实数范围内不能表示成两个整数之比的数。 简单的说，无理数就是10进制下的无限不循环小数，如圆周率、√2等。也是开方开不尽的数。（3）无理数和有理数共同组建了实数，实数，是有理数和无理数的总称。数学上，实数定义为与数轴上的点相对应的数。

〖D〗、正有理数指的是数学术语，除了负数、0、无理数的数字，正有理数能精确地表示为两个整数之比。负有理数就是小于零并能用小数表示的数。如 -123， -..。

初一数学有理数概念概括整理

〖A〗、有理数是能够表示成两个整数之比的数，包括整数，有限小数和无限循环小数 整数和分数统称为有理数，任何一个有理数都可以写成分数m/n（m，n都是整数，m，n互质，且n≠0）的形式。从而有理数又称作分数。

〖B〗、在以前学过的0以外的数前面加上负号“—”的数叫负数（negative number）。 与负数具有相反意义，即以前学过的0以外的数叫做正数（positive number）（根据需要，有时在正数前面也加上“+”）。 2 有理数 正整数、0、负整数统称整数（integer），正分数和负分数统称分数（fraction）。

〖C〗、第二章 有理数数轴：数轴三要素：原点，正方向和单位长度；数轴上的点与实数是一一对应的。相反数实数a的相反数是-a；若a与b互为相反数，则有a+b=0，反之亦然；几何意义：在数轴上，表示相反数的两个点位于原点的两侧，并且到原点的距离相等。倒数：若两个数的积等于1，则这两个数互为倒数。

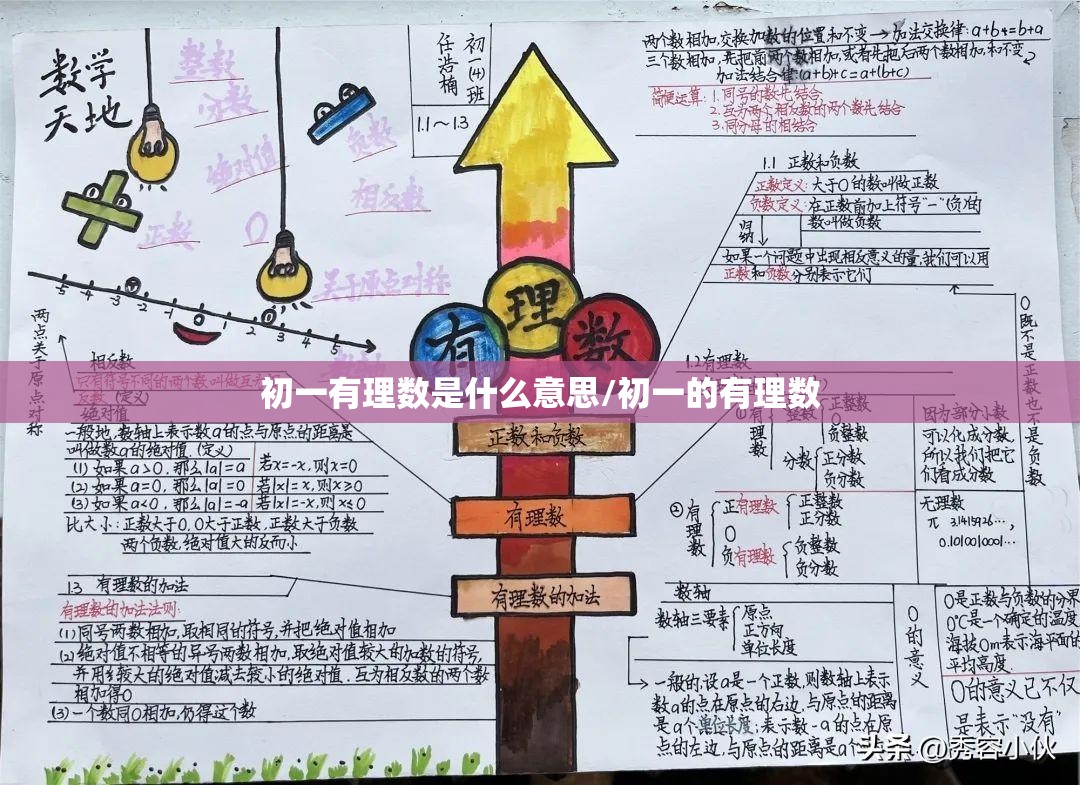
〖D〗、全书知识总结框架图（简易版）该简易版思维导图概括了七年级上册数学的四个主要单元：有理数、整式的加减、一元一次方程、几何图形初步。每个单元下都包含了该单元的核心知识点。