有理数是什么意思
有理数之所以被称为有理数,是因为其小数表示具有规律性,这里的“理”指的是规律。具体来说:规律性:有理数的小数表示可以是有限的,也可以是无限循环的。这种小数表示上的规律性是有理数的一个重要特征。对比无理数:与有理数相对的是无理数,无理数的小数部分是无限不循环的,没有明确的规律可循,例如根号2的值就是一个典型的无理数。
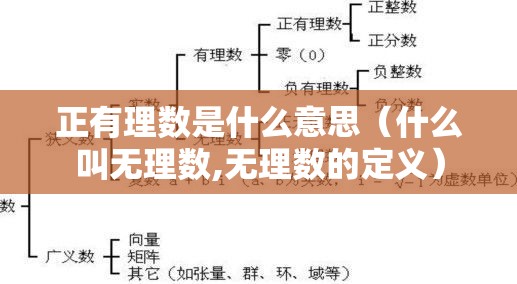
有理数是整数和分数的统称,有理数是一个整数a和一个正整数b的比,例如:5,33,81/100,1/9,-5等等。
有理数是可以表示为两个整数之比的数,包括整数和分数;无理数则是不能表示为两个整数之比的实数,其小数部分是无限不循环的。有理数: 定义:有理数是整数和分数的统称,即可以表示为两个整数之比的数。 表示:整数可以看作分母为1的分数,因此整数也属于有理数的范畴。
有理数是可以表示为两个整数比值的数,无理数则是不能表示为两个整数比值的数。有理数:包括整数和分数,它们的小数部分要么是有限的,要么是无限循环的。有理数可以精确地表示为两个整数的比值,例如4可以表示为4/1,1/3的小数形式为0.33333……。
有理数是整数(正整数、0、负整数)和分数的统称,是整数和分数的集合。整数也可看做是分母为一的分数。不是有理数的实数称为无理数,即无理数的小数部分是无限不循环的数。无理数,也称为无限不循环小数,不能写作两整数之比。
正有理数是什么意思?
正有理数指的是数学术语,除了负数、0、无理数的数字,正有理数能精确地表示为两个整数之比。负有理数就是小于零并能用小数表示的数。如 -123, -..。
有理数:是一个广泛的分类,包括了正有理数、负有理数和零。正有理数:是正数中的一种特定类型,即大于零的有理数,不包括零和负数。综上所述,正有理数是有理数的一个子集,它们都是可以表示为分数的数,但正有理数是严格大于零的,而一般的有理数则包括了所有正数、负数和零。
正有理数:正有理数是指所有大于零的有理数,包括正整数和正分数。正整数是自然数,如4等,而正分数是可以写成两个整数的比例,例如1/3/5/6等。正有理数可以表示为分数形式,其中分子和分母都是正整数。
除了负数、0、无理数的数字都是正有理数。正有理数能精确地表示为两个整数之比。有理数为整数(正整数、0、负整数)和分数的统称。正整数和正分数合称为正有理数,负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。
正有理数包括正整数和正分数。具体解释如下:正整数:正整数是大于0的整数,例如4……等。它们是正有理数的一个重要组成部分,因为任何正整数都可以看作是其自身与1的比值,即形如$frac{n}{1}$(n为正整数)的有理数。
有理数是什么意思?例如哪些数是有理数?
〖A〗、有理数是整数和分数的统称,有理数是一个整数a和一个正整数b的比,例如:5,33,81/100,1/9,-5等等。
〖B〗、有理数是可以表示为有限小数或无限循环小数的数,例如1/3=0.333333……就是无限循环小数。所有的整数都是有理数,因为它们都可以表示为分数(如1/2,-3等)。有理数还可以分为正有理数、负有理数和零。
〖C〗、有理数为整数(正整数 0、负整数)和分数的统称。正整数和正分数合称为正有理数,负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。有理数的定义 有理数有两种分类,分别是正有理数,包括正整数和正分数;负有理数,包括负整数和负分数。

〖D〗、能够表示成分数的数是有理数:1=1/1 2=2/1 2/3 -12=-12/1 0 =0/1 0.3=3/10 0.33333 -0.999 凡是整数、0、有限小数、无限循环小数全是有理数 有理数的概念=分数的概念。
〖E〗、有理数:定义:有理数是整数和分数的集合,整数也可看做是分母为一的分数。特性:有理数的小数部分是有限或为无限循环的数。例如,1/0.0.333都是有理数。无理数:定义:无理数也称为无限不循环小数,不能写作两整数之比。特性:无理数的小数部分是无限且不循环的。

〖F〗、实数,是有理数和无理数的总称。数学上,实数定义为与数轴上的实数,点相对应的数。实数可以直观地看作有限小数与无限小数,实数和数轴上的点一一对应。但仅仅以列举的方式不能描述实数的整体。实数和虚数共同构成复数。实数可以分为有理数和无理数两类,或代数数和超越数两类。
正有理数的定义是什么?
除了负数、0、无理数的数字都是正有理数。正有理数能精确地表示为两个整数之比。有理数为整数(正整数、0、负整数)和分数的统称。正整数和正分数合称为正有理数,负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。命名由来 “有理数”这一名称不免叫人费解,有理数并不比别的数更“有道理”。
有理数:是一个广泛的分类,包括了正有理数、负有理数和零。正有理数:是正数中的一种特定类型,即大于零的有理数,不包括零和负数。综上所述,正有理数是有理数的一个子集,它们都是可以表示为分数的数,但正有理数是严格大于零的,而一般的有理数则包括了所有正数、负数和零。
正有理数指的是数学术语,除了负数、0、无理数的数字,正有理数能精确地表示为两个整数之比。负有理数就是小于零并能用小数表示的数。如 -123, -..。
正有理数指的是可以表示成两个整数商的正数,如1/3/5/6等。那么正有理数如何进行分类呢?第一类正有理数:整数。整数指的是不带小数部分的数字,例如1,2,3,4等。整数可以表示为n/1的形式,其中n为整数。所以整数也是正有理数。第二类正有理数:带分数。
定义:正有理数是指大于0的有理数,即这些数可以表示为两个整数的比,并且结果大于0。构成:正有理数包括正整数、正分数,以及大于0的有限小数和无限循环小数。性质:正有理数属于有理数集Q,是实数集的一个子集。它们具备进行四则运算的性质,且没有最大的正有理数。

 微信扫一扫打赏
微信扫一扫打赏

